Paralaxe Trigonométrica

Conheça essa técnica engenhosa e simples para se conhecer as distâncias que nos separam de muitas estrelas.

Um dos problemas astronômicos mais antigos é a determinação de distâncias no espaço. Existem várias técnicas para se resolver esse problema, e cada uma delas se aplica melhor a determinados casos. Um método bastante interessante por sua simplicidade é conhecido como paralaxe trigonométrica, ou, simplesmente, método da paralaxe. Com conceitos extremamente simples de geometria, podemos determinar as distâncias que nos separam de muitas estrelas.

A palavra paralaxe vem do grego, e significa algo como alteração. Podemos entender paralaxe como a modificação aparente da posição de um objeto em relação a outro objeto mais distante, devido à modificação real da posição do observador. Com certeza isso é bem mais simples do que parece. Vamos fazer uma rápida experiência para entender paralaxe.

Aí mesmo onde o leitor está, escolha algum objeto distante. Se estiver em uma sala, pode ser uma janela na parede oposta, um quadro, ou a maçaneta da porta. Se estiver lendo esse artigo em um local aberto, pode ser uma árvore, uma ilha no mar, qualquer objeto relativamente distante. Escolheu? Agora feche um olho e cubra esse objeto com um dedo ou algo que possa segurar bem mais próximo que o objeto distante escolhido. Talvez uma caneta. Cobriu o objeto distante como objeto próximo? Agora simplesmente balance ligeiramente a cabeça para um lado e para o outro. Viu seu dedo, ou o que estava segurando próximo a você se deslocar em relação ao objeto distante que você escolheu como referência? Se você conseguiu verificar isso, então entendeu o conceito de paralaxe.

A figura abaixo representa esse mesmo deslocamento aparente entre um objeto próximo e um fundo com objetos distantes.

Essa experiência pode parecer banal, mas devido a esse deslocamento aparente provocado pela mudança de posição do observador, conseguimos conhecer distâncias astronômicas de maneira assustadoramente simples. Vejamos como isso funciona.

Lembra do objeto distante que você escolheu? Imagine que esse objeto seja uma estrela bastante distante. O objeto mais próximo de você será agora uma outra estrela, mais próxima que a primeira. Por fim, em vez de balançar sua cabeça, o deslocamento do observador será o deslocamento da Terra ao redor do Sol.

Assim, uma noite você mede a distância angular entre as duas estrelas. Seis meses depois, quando a Terra estiver na posição oposta em sua órbita, você faz a mesma coisa. Dessa forma, você terá duas medidas angulares diferentes. A figura abaixo está fora de escala para exemplificar as configurações geométricas entre Terra, Sol e as duas estrelas envolvidas.

Agora vamos utilizar um artifício matemático que pode parecer mágica, mas eu garanto que não é. A estrela de fundo está muito distante, de modo que podemos considerá-la no infinito. A matemática nos diz que retas paralelas se encontram no infinito. Se colocarmos a nossa estrela de referência realmente no infinito, podemos representar os ângulos medidos da seguinte forma:

Os ângulos A₁ e p₁ são alternos internos, assim como A₂ e p₂. Isso significa que A₂=p₂ e A₁=p₁. Com isso, podemos desenhar a seguinte figura:

Temos, assim, um triângulo retângulo, cujos vértices são Sol, Terra e a estrela cuja distância queremos determinar. O tamanho do lado u.a. nada mais é que a distância da Terra ao Sol, conhecida como unidade astronômica (em alguns livros pode aparecer a sigla a.u., do inglês astronomical unit). Uma unidade astronômica vale aproximadamente 150 milhões de quilômetros.

O ângulo p da Figura 4 é metade do ângulo formado por p₁ e p₂ na Figura 3. Como vimos, p₁=A₁ e p₂=A₂, sendo que A₁ e A₂ são os ângulos que medimos diretamente. Dessa forma, podemos encontrar o ângulo p:

Conhecendo p e o valor da unidade astronômica, podemos relacioná-los com a distância d, que queremos encontrar, através da tangente de p:

Agora, podemos fazer uso de mais duas aproximações matemáticas. Perceba que as figuras 2 e 4 estão propositadamente fora de escala, para representarmos de maneira inteligível um sistema Sol-Terra-estrela e os alinhamentos que nos interessam. Todas as estrelas, inclusive a mais próxima, estão tão distantes do Sistema Solar que a distância entre a Terra e o Sol é perfeitamente desprezível. Repare na Figura 5 o que acontece com nosso triângulo retângulo quando colocamos a estrela, cuja distância queremos determinar, bem mais distante que a Terra e o Sol:

Ainda assim, a Figura 5 está longe da proporção correta se levássemos em conta a distância verdadeira de qualquer estrela. Mas já é possível perceber que na situação real, teremos um triângulo retângulo tal que a hipotenusa h tem tamanho muito próximo ao do cateto d. Assim, em vez de utilizarmos a tangente de p, que relaciona o ângulo com os catetos do triângulo, podemos utilizar o seno de p, que relaciona o ângulo, o cateto oposto e a hipotenusa:

onde já fizemos a aproximação h~d. Agora vamos ao segundo recurso matemático: senos de ângulos muito pequenos podem ser aproximados para o próprio ângulo. A Figura 5 nos dá uma idéia de que o ângulo p deve ser realmente muito pequeno, e, de fato, é muito pequeno em medidas reais. Assim, a distância entre a estrela e o Sol (ou a Terra, pois, como vimos, a distância entre a Terra e o Sol é desprezível nessa escala), é dada por:

Para efeitos aritméticos, o ângulo p deve sempre ser dado em radianos.

As distâncias astronômicas são sempre muito maiores do que as distâncias que temos contato cotidianamente. Se você acha que seu trabalho ou escola fica longe de sua casa, talvez seja um bom consolo dar uma olhadinha nas distâncias astronômicas…

As aproximações que fizemos para encontrar a fórmula simples de determinação de distâncias através da paralaxe só são possíveis por causa dos grandes valores de distâncias envolvidos. Muitas vezes essas distâncias são tão grandes que é complicado expressá-las em metros ou quilômetros. Para isso, criamos novas unidades de medidas astronômicas. A mais famosa é o ano-luz, que é igual à distância percorrida pela luz, no vácuo, em um ano. Equivale a aproximadamente nove trilhões de quilômetros.

Outra unidade muito utilizada em Astronomia é o parsec, que é definido como a distância relativa à paralaxe de um segundo de arco. Agora que sabemos como determinar distâncias utilizando o método da paralaxe trigonométrica, podemos encontrar quanto vale um parsec em alguma outra unidade de medida, como quilômetro ou ano-luz. Para isso, vamos encontrar qual a distância d para uma paralaxe p=1’’ (as linhas acima do número denotam um segundo de arco).

Para utilizarmos a fórmula (4) na forma como está escrita, devemos escrever um segundo de arco em radianos. Sabendo que um grau tem sessenta minutos, um minuto tem sessenta segundos, e que PI radianos tem 180 graus, temos que

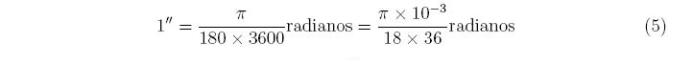
Uma unidade astronômica vale aproximadamente 15 X 10⁷km, e com a fórmula (5) encontramos quantos quilômetros tem um parsec:

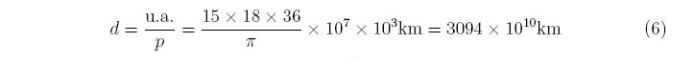
Esse valor é muito grande, e não facilita nada o trabalho numérico nem permite uma comparação útil do parsec com outra unidade de medida. Por isso, em geral, se faz uma correspondência do parsec com o ano-luz.

Podemos pegar o valor do parsec em quilômetros e convertê-lo para anos-luz, ou utilizarmos a fórmula (5) com o valor da unidade astronômica em anos-luz. Para isso, devemos saber que um ano-luz vale 9,460 X10¹²km, de modo que podemos escrever a unidade astronômica como 1,58 X10^-5 ano-luz. Assim:

Esse é o valor do parsec em anos-luz. Dessa forma, fica simples se comparar uma distância dada em parsecs com seu valor correspondente em anos-luz.